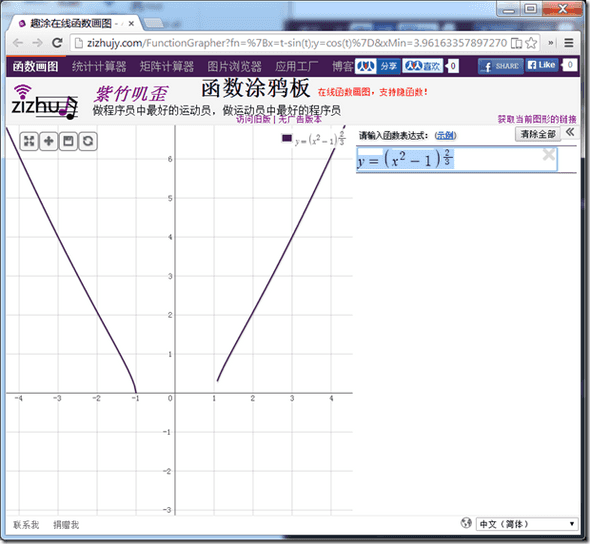
问题：

对于一个分数，使用除法就能够得到其小数表示。如：

2/3 = 0.666666…

一般计算器都支持将分数转化成小数的计算模式。但是反过来，拿到一个小数，怎么得到其分数的表示形式呢？似乎没有像除法这样直接的算法，而且一般的计算器和计算程序都没有将分数转化成小数的模式。

比如，拿到一个小数：0.571428571428…，怎么知道它等于4/7？

分析：

小数可分为以下几种：

  • 有限小数，如0.5678，
  • 无限循环小数，如刚才的例子：0.571428571428…
  • 无限不循环小数，如：3.141592654…（π）

对于第一种，有限小数，转化成分数很简单，比如：

0.5678 （共4位小数，把它乘以10的4次方，再除以10的4次方）

= 5678 / 10000 （约分到最简——找出分子分母的最大公约数，同除之）

= 2839 / 5000

对于第二种，无限循环小数，先找到循环节，然后将这个小数按照这些循环节拆成小限小数，而这个小数本身是这些无限个有限小数的和。比如：

0.571428571428…

（循环节是571428）

= 0.571428 + 0.000000571428 + 0.000000000000571428 + …

（再进行一些数学计算，会简化出一个模式来）

= 571428 * 10-6 + 571428 * 10-12 + 571428 * 10-18 + …

= 571428 * (10-6 + (10-6)2 + (10-6)3 + …)

注意到无限小数就是一个以循环节为整数的数乘以一个无限等比数列（公比是10-6，公比小于1。这个数列好像叫做级数？）的和，而这个级数和，正好可以算出一个精确的分数值（首项 / (1 - 首项)）。将它们相乘，再约分，即能得到最终我们想要的分数值。接上面的等式：

= 571428 * (10-6 / (1 - 10-6))

= 571428 * (1 / 999999)

= 571428 / 999999

= 4 / 7

对于第三种，无限不循环小数，没有办法转化成一个分数。事实上，有限小数和无限循环小数都是有理数，而这个无限不循环小数得无理数。有理数可以写成分数形式，而无理数是不可以的。它们是属于两个不同的世界。

总结：

有理数小数可以转化成分数形式，而无理数小数则不行。

对于有限小数，转化成分数的方法是：

  1. 数出其小数位数（有效小数位数）n
  2. 以10为底，计算10的n次方作为因子
  3. 对小数乘以这个因子作为分子，将因子作为分母
  4. 约分化简
  5. 完成

对于无限循环小数 ，转化成分数的方法是：

  1. 找出循环节，将它作为一个整数m，并作为分子
  2. 数出这个循环节的位数n
  3. 以10为底，计算10的n次方作为因子
  4. 将这个因子减去1，作为分母
  5. 约分化简
  6. 完成

对于无限不循环小数，无法转化成分数。不过这里留一个问题：是否有可能找到一种方法，将其转化成精确的无理数表示形式？比如：

  • 3.141592654… –> π
  • 1.414213562… –> 2的平方根
  • 等等

实际用途：

在《对JavaScript的Math.pow()函数的一个修正》中提到，JavaScript的Math.pow()不能够计算诸如(-27)^(1/3)等负数的奇次方根。

该文给出的修正方案解决了这个问题，但是使用该方案仍然不能够求出(-27)^(2/3)（实际得到结果 NaN，我们期待得到结果 9）。

要解决这个新的问题，便需要使用小数转化成分数的方法（前文中的方案只是对小数求倒数，看它是否是1/n，若是并且当n是奇数时，进行一下特殊处理以计算出期待的结果；若n是偶数，则计算不出结果或结果是 NaN 是合理的，因为负数没有偶数次方根）。

具体原因和具体解决方案，后面的博文继续介绍。大概情况是，当在JavaScript中求 Math.pow(-27, 2/3)时，传给Math.pow()函数的2/3这个参数，在到达函数体时已经被存储成了小数，在这个函数体里，需要尝试将这个小数转换成分数，若转换成功，则计算出结果，比如9。若转换不成功，则说明这个小数是无理数，那么给出结果 NaN 是合理的（一个数的无理数次方，没有定义是比较正常的吧）。

当然，JavaScript只存储小数的有限数位，所以，对于这个理想的转换方法，在JavaScript中还需要进行一些奇怪的处理：只要一个小数看上去像是一个无限循环小数，那么就将其当成真的是无限循环小数，然后应用总结中的算法，将其转换成分数。

有了这些之后，函数涂鸦板便能正确画出类似这种函数的图形了：

y=(x2-1)2/3

目前函数涂鸦板画出的它的图形在（-1 < x < 1）的范围里不正确，原因就是因为JavaScript的 Math.pow() 函数的缺陷。

$y=\left(x^2-1\right)^{\frac{2}{3}}$ 的不正确的图形

这个修正即将上线，正确的图形马上就要出来了！

$y=\left(x^2-1\right)^{\frac{2}{3}}$ 的正确的图形

附（等比数列求和算法）：

【定理1】数列 {q, q2, q3, …, qn} 的和为 S = (q + q(n+1)) / (1 - q)。

【证明】

（1）S = q + q2 + … + qn

q * S = q * (q + q2 + … + qn)，即

（2）q * S = q2 + q3 + … + q(n+1)

（1）式与（2）式两边同时相减

S – q * S = (q + q2 + … + qn) – (q2 + q3 + … + q(n+1))

即：

(1 - q) * S = q + (q2 – q2) + (q3 – q3) + … (qn – qn) + q(n+1)

(1 – q) * S = q + q(n+1)

所以：

S = (q + q(n+1)) / (1 - q)

【证毕】

【定理2】级数 {q, q2, …, qn, …} （0 < q < 1）的和为 S = q / (1-q)。

【证明】

【证法1】对【定理1】对n—>无穷大取极限。

【证法2】如法炮制【定理1】的证明过程：

（1）S = q + q2 + … + qn + …

q * S = q * (q + q2 + … + qn + …)，即

（2）q * S = q2 + q3 + … + q(n+1) + …

（1）式与（2）式两边同时相减

S – q * S = (q + q2 + … + qn + …) – (q2 + q3 + … + q(n+1) + …)

即：

(1 - q) * S = q + (q2 – q2) + (q3 – q3) + … (qn – qn) + …

(1 – q) * S = q

所以：

S = q / (1 - q)

【证毕】